zero-sum game solved in Matlab

In Zero-Sum games, a player can win, only if the other player looses. Rock-paper-scissors is a typical example of a zero-sum game. These games can be solved with Linear Programming (LP) because the latter has duals. So, how to solve this game in Matlab? This post is an extension to my previous post dealing with LP. The problem is to minimize a function z = f(rock,paper,scissors) = f (x1,x2,x3) equal to some payoff value v, subject to the following game conditions:

   -------->    

to solve in Matlab, we must rearrange the constraints to include v as a variable (right). The game matrix is:

A = [0 -1 1 1; 1 0 -1 1; -1 1 0 1];
b = [0 0 0];
Aeq = [1 1 1 0];
beq = 1;
lb = [0 0 0 -inf]; % here the lower bound of v has not to necessarily zero, but in a general game could be minus infinity. 
% Objective function
f = [0 0 0 -1];
% Solve the LP 
z = linprog(f,A,b,Aeq,beq,lb);
% Payoff 
v = z(4)
% Probability of the variables 
x = z(1:3)


v =
     0

x =
    0.3333
    0.3333
    0.3333

Solving Linear Programming problems with several constraint types in Matlab

The most difficult part of linear programming is the model building. However, once the model is clearly stated, the constraints may be a challenge. It might be the case that some constraints are less than some constant while others are larger than some constant, and even other are equal to a coefficient. In addition, it is important to keep in mind that the Matlab routine linprog is devised to solve minimization problems, not maximization. So before solving the problem, we have to make sure that all the constraints and equalities, etc. are consistent with the input structure of linprog in Matlab. In order to show this I prepared a short handout and I also work a textbook example for illustration purposes.
Suppose that we want to minimize an objective function f  subject to the following constraints:

Here we have all the possible constraint cases. Remember that Matlab solves cases in the form:

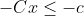
So we only have to transform the C constraint to , to look like the Matlab formulation. In Matlab code it would look like:

[x,~,~,~,lambda] = linprog(f,[A;-C],[a;c],Beq,beq,lb,ub);

where Beq and beq denote the equality for the B constraint. 
Now let's work a more complicated example from the book Mathematical Models in Agriculture by J.  Thornley and J. France, p. 69-75.
Minimize the following objective function

subject to the following constraints:

A way to solve this in Matlab would be:

f = [6.6 9 36 14.9 65]; f = f(:);
A = [13.7 14.2 11.1 12.3 0;
    108 98 701 503 0;
     .5 .2 79.3 2.3 120;
     3.8 2.7 43.7 10.2 60;
     .2 .1 16.1 5 60;
     1.3 1 2.2 3.1 30];
a = [13 160 7 7 3 2]; b = b(:);
Aeq = [1 1 1 1 1]; % The equality constraint
beq = 1;
lb = [0 .1 0 0 .01]; lb = lb(:); % The lower bounds. Note that  it includes all three at the same time (i.e. x2>.1; x5>.01 and x1,3,4 >= 0) 
[x,~,~,~,lambda] = linprog(f,-A,-a,Aeq,beq,lb);
% Don't forget that to change the sign of Ax>=a both, A and a have to be negative.

Results

x =
      0.74423
          0.1
     0.034488
     0.090751
     0.030536

profit z is:


>> z = f'*x
y_dual = lambda.ineqlin

z =
       10.39
y_dual =
            0
     0.011666
      0.14076
            0
      0.71638
            0