Pons Asinorum in Logic

Pons Asinorum. Kneale & Kneale 186

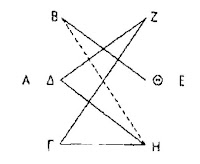
Kneale and Kneale, p. 186-187 explain: "Aristotle suggests a technique for finding syllogisms to prove conclusions of the four different kinds. When we want to prove a universal affirmative conclusion with two given terms, we should consider characters which entail the predicate of the proposed conclusion and characters which are entailed by the subject of the proposed conclusion. When we want to prove a particular affirmative we should consider characters which entail the predicate and characters which entail the subject. When we want to prove a universal negative we should consider characters which are incompatible with the predicate and characters which are entailed by the subject or conversely characters which are entailed by the predicate and characters which are incompatible with the subject. And finally, when we want to prove a particular negative we should consider characters which are incompatible with the predicate and characters which entail the subject. ... The diagram which Alexander [of Aphrodisias] describes is not preserved in our text of his work, but it can easily be reconstructed as shown, According to Aristotle's lettering, A is the predicate of the conclusion, B the group of characters entailed by A, Γ the group of characters that entail A, Δ the group of characters incompatible with A, E the subject of the conclusion, and Z, H, Θ the groups of characters related to it in the same way as the groups opposite are related to A. We have inserted five continuous lines to represent the five cases noticed above (two for the proof of universal negative conclusions) and a dotted line to represent the case--{Baralipton) in which we can prove a particular affirmative conclusion from premisses that would suffice to prove the universal affirmative with transposed terms."

A nicer pons asinorum from the 17th century. Source unknown