Analogy is a kind of similarity in which the same system of relations holds across different objects (Gentner p.107) ...
"the ability to carry out fluent, apparently effortless, structural alignment and mapping [is] a hallmark of human cognitive processing" (Gentner and Markman 1997, p. 53).
Assume that an element S, to be used in an analogy has, say, 4 properties, i,j,k,l. Each of these properties sufficiently define the element S. Let's represent it by:
In an analogy there are at least 2 elements to be compared. Say the other element is C with properties k,l,m,n.
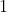 \quad S_{i,j,k,l} \stackrel{(k,l)}{=} C_{k,l,m,n} "1) \quad S_{i,j,k,l} \stackrel{(k,l)}{=} C_{k,l,m,n}")
"the ability to carry out fluent, apparently effortless, structural alignment and mapping [is] a hallmark of human cognitive processing" (Gentner and Markman 1997, p. 53).
Assume that an element S, to be used in an analogy has, say, 4 properties, i,j,k,l. Each of these properties sufficiently define the element S. Let's represent it by:
To compare both elements in an analogy, let's define an analogy operator }{=} "\stackrel{(k,l)}{=}")
which tells that both elements share properties k and l. i.e.
Result 1: The most basic result of an analogy is that both elements can be equaled only in the properties that they share. In the example, we can say that S is like C in k and l, only. Any other inference of the remaining properties of either element is not supported by the analogy and constitutes automatically in the fallacy of false analogy.
Another situation involves the assumption that "the predication is transitive across two analogies" (Lightbody and Berman, 2010). In other words, this involves
However this does not always hold because each element has properties unlike the previous example. Let's propose another analogy with S
We want to check if P is like C since S = C and S = P. In order to investigate the feasibility of such deductive inference, we now need to determine if the "analogizers" overlap (i.e. the properties overlap) in order to allow a deductive inference. However,
}{=} \not\equiv \stackrel{(i,j)}{=} "\stackrel{(k,l)}{=} \not\equiv \stackrel{(i,j)}{=}")
Since the "analogizers" are not equivalent, therefore any further deductive parallel between C and P is not valid, i.e.:
We can say nothing about the relationship between C and P because ther properties allow us not to move in that direction.
Result 2: In a crossed analogy, if the properties of the predicates do not overlap, then the deduction cannot be carried out. If this rule is violated, the Metaphoric Fallacy by Deductive Inference (MFDI) is incurred (Lightbody and Berman, 2010).
Yet another possibility easily extensible from previous results is that of comparing two analogies and infer something from the last one, like A = B as C = D. In this case we need to compare the analogy operators of both analogies and check what's overlapped, i.e.
}{=} & B_{j,k,l} \\ C_{k,u,w}& \stackrel{(k,u)}{=} & D_{k,u,x} \\ \end{matrix} "\large \begin{matrix} A_{i,j,k}& \stackrel{(j,k)}{=} & B_{j,k,l} \\ C_{k,u,w}& \stackrel{(k,u)}{=} & D_{k,u,x} \\ \end{matrix}")
therefore both analogies are not entirely comparable but only through the k property
}{=}\; {\color{Red} \stackrel{(k)}{\equiv}} \;\stackrel{(k,u)}{=} "\large \stackrel{(j,k)}{=}\; {\color{Red} \stackrel{(k)}{\equiv}} \;\stackrel{(k,u)}{=}")
We are then allowed to read that as: A is to B as C is to D, in the k property only. We can simplify the notation of the previous equation as:
} \stackrel{(k)}{\equiv} \overline{CD}_{(k,u)} "\large \overline{AB}_{(j,k)} \stackrel{(k)}{\equiv} \overline{CD}_{(k,u)}")
This result is a generalization of Result 1. However, its the degree of certainty might be less because the joint properties of the analogy might have "degraded" since they come from two elements.
One can never be sure that has grasped all possible properties of an element in an analogy. This brings us to one of the main goals of analogies, to hypothesize about the presence of hidden properties in an element based on the analogy-based argument. On which grounds this can be valid? Symbolically
}{=} \mathit{B}_{i,j,{\color{Red} m}} "\large \mathit{A}_{i,j,k,{\color{Red} ...}} \stackrel{(i,j)}{=} \mathit{B}_{i,j,{\color{Red} m}}")
The question is if the (i,j) matched properties, afford the hypothesis that B's m is a "hidden property" of A. Can I hypothesize the presence of "m" as hidden given the strength of (i,j)? This inference is inductive and as such must be accompanied by a modal qualifier. Actually in Toulmin's scheme, (i,j) constitutes the warrants on which the syllogism stands, "m belongs to A" is the conclusion, and "A is like B" is the grounds. But a modal qualifier has to be there.
The number and importance of the dimensions that coincide between both candidates is an indicator of the "weakness" or "strongness" of the equivalence. If both elements shared a single element in common, then the equivalence would be possible, but only in that single dimension that both elements share.
therefore both analogies are not entirely comparable but only through the k property
We are then allowed to read that as: A is to B as C is to D, in the k property only. We can simplify the notation of the previous equation as:
This result is a generalization of Result 1. However, its the degree of certainty might be less because the joint properties of the analogy might have "degraded" since they come from two elements.
Features of the analogy operator.
The operator defines if an analogy is valid (feasibility), and on which properties is valid (extent). However there's more to it. These two features of the analogy aim at answering two questions:
Feasibility: Is the analogy at all possible?
Extent: Does the analogy capture the most important properties of the elements? On which grounds the analogy holds?
Strength: What's the descriptive power of the analogy? Is it weak, mild, strong? are the properties qualitative or quantitative?
While the analogy operator sheds light on the feasibility and the extent of the analogy, it does not say much about the strength of the comparison. An appraisal of the degree of match between the properties is needed to elucidate the strength of the analogy. The match can be qualitative or quantitative depending on the nature of the properties.
Uncertainty in the number of element properties
One can never be sure that has grasped all possible properties of an element in an analogy. This brings us to one of the main goals of analogies, to hypothesize about the presence of hidden properties in an element based on the analogy-based argument. On which grounds this can be valid? Symbolically
Examples
As an example let's consider Phaedo's proof of the immortality of the soul:
1) "sleep" precedes "being awake" and also, "being awake" precedes "sleep"
2) "death" is like sleeping and "living" is like being awake.
3) "being awake" precedes "living"
4) Because of (1) to (3), therefore (4) can be completed by stating that: "dead" precedes "to live", i.e. everybody has been dead before being born.
Let's define the properties of each element. Sleep-Awake (SA) have: domain: temporal (is a natural process), function: circular (both precede each other), iconic: used as a metaphor. Symbolically:
the other element is the dyad dead-alive (DA) whose properties are: domain: timelessness (ts), function: what Socrates wants to prove, iconic: used as a metaphor, i.e.
The analogy only holds by its iconic property. However there are some problems for the analogy to hold. First the domain properties are in conflict. Seems hard to prove that what occurs in a natural process also holds in a metaphysical, timeless realm. In addition, the argument lacks of any modal qualifier to moderate the inductive inference that assigns the "circularity" of the sleep-awake process to the death-life process. The iconic property alone does not justify such an inference plus the heavy doubts cast by natural process holding in a metaphysical realm. Thus this constitutes a fallacy.
}{=} \mathit{DA}_{ts,?,i} "\large \mathit{SA}_{t,c,i} \stackrel{(i)}{=} \mathit{DA}_{ts,?,i}")
The number and importance of the dimensions that coincide between both candidates is an indicator of the "weakness" or "strongness" of the equivalence. If both elements shared a single element in common, then the equivalence would be possible, but only in that single dimension that both elements share.
A more general case would be that one of the elements has more dimensions than the other, i.e.
References:
Gentner, D. (1998). Analogy. In W. Bechtel & G. Graham (Eds.), A companion to cognitive
science (pp. 107-113). Oxford: Blackwell
Gentner, D. and Markman, A. B. (1997): "Structure Mapping in Analogy and Similarity,"
American Psychologist, 52, 45-56.
No comments:
Post a Comment