Growth Models Survey

Growth models are tools to describe the increase in a variable as a function of another variable. I'll post here some models that I've came across along with a short explanation.

Exponential Growth Model

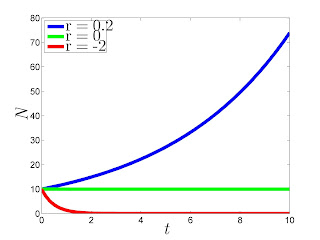
The number of units Nt (e.g. organisms) in time t (or next t generations), is proportional to its initial number of units N0 and the instantaneous growth rate r, i.e.

$\large N_t = N_0 \times e^{rt}$

If r > 0, N increases. If r < 0, N decreases. If r = 0, N = N0. Parameter r can be interpreted as a difference between births rate (b) and mortality rate (m). By taking derivative of Nt we have:

$\large \frac{dN_t}{dt} = rN_0=(b-m)N_0$

References:
Sharov, A. website
https://www.math.duke.edu/education/postcalc/growth/growth4_6.html

Logistic Model
3-Parameter

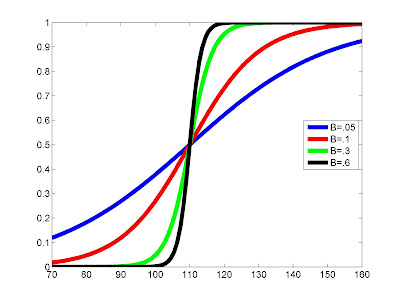The model equation is:

$\large y = \frac{C}{1+Ae^{-Bx}}$

where C is the limiting value, B has no easy interpretation but is related to the spread of the curve in the x-axis and A is a constant related to the origin of coordinates. If the x is chosen so that x = 0 corresponds to the inflection point, then A = 1.
This model is symmetric around the inflection point which occurs at C / 2. This means that the curve's 2 branches are equal. The derivative, if A = 1, is

dy/dx for the graph above

$\large \frac{dy}{dx}=\frac{B\, C}{\mathrm{e}^{B\, x}\, {\left(\mathrm{e}^{- B\, x} + 1\right)}^2}$

If A ≠ 1, then the inflection point coordinates are located at (x,y) = ((lnA)/B, C/2) and dx/dy is:

$\large \frac{dy}{dx}=\frac{A\, B\, C}{\mathrm{e}^{B\, x}\, {\left(\displaystyle\frac{A}{\mathrm{e}^{B\, x}} + 1\right)}^2}$
References:

http://www.cs.xu.edu/math/math120/01f/logistic.pdf
Richards, F.J. (1959), A Flexible Growth Function for Empirical Use, J. Exp. Bot. (1959) 10 (2): 290-301.
Good website on Population Growth Models: here

(to be continued...)

Enthumematon - ἐνθυμημάτων

Labels

Growth Models Survey

No comments:

Post a Comment